Views: 37
O Algoritmo do Quake 3 que Revolucionou os Jogos
Muitos podem não estar familiarizados com a franquia Quake, muito menos com sua importância no mundo dos jogos. Embora tenha perdido destaque ao longo do tempo diante de outras séries, sua relevância não foi esquecida. Podemos afirmar que a evolução da renderização 3D deve muito ao legado do Quake 3.
Contextualizando
Quake 3 Arena foi um marco nos jogos de tiro em primeira pessoa, lançado em 1999 pela id Software. Ele se destacava pela rápida movimentação e intensos tiroteios. O jogo emergiu durante o que pode ser chamado de “era de ouro do boomer shooter”, quando o gênero estava no auge.
Em 2005, a id Software disponibilizou o código fonte do Quake III Arena para o público. Durante a análise desse código, foi descoberto um algoritmo tão engenhoso que estava à frente de seu tempo. Mesmo após seis anos de avanços tecnológicos e desde o lançamento original do jogo, essa descoberta se tornou padrão no desenvolvimento de jogos AAA.
Esse algoritmo incrível calcula o inverso da raiz quadrada. Se precisasse escrever um trecho de código em C que realizasse esse cálculo da maneira mais prática e comum, seria algo assim:

Porém, nos deparamos com um desafio significativo: o cálculo da raiz quadrada é lento e a divisão não é muito mais eficiente.
Perante essas adversidades, surgiu a necessidade de criar um algoritmo mais rápido e eficiente que pudesse substituir o método habitual de realizar essas operações computacionalmente custosas, como a raiz quadrada e a divisão. Os criadores da linguagem C, cientes desses desafios, desenvolveram uma abordagem nativa para esses cálculos dentro do próprio C, inclusa na biblioteca padrão <math.h>. No entanto, mesmo essa abordagem nativa enfrentava limitações de desempenho devido à natureza computacionalmente intensiva dessas operações.
Para superar essas limitações, os desenvolvedores precisavam de um algoritmo mais rápido e eficiente. Assim, foi criado um algoritmo que oferecia uma alternativa mais ágil às operações de raiz quadrada e divisão. Este algoritmo engenhoso foi incorporado ao código-fonte do Quake III Arena, onde se mostrou excepcionalmente eficaz, mesmo em face dos desafios tecnológicos da época.
Esse algoritmo revolucionário não apenas permitiu um desempenho aprimorado dentro do jogo, mas também influenciou significativamente o desenvolvimento de jogos e aplicações em toda a indústria, mostrando-se como um exemplo brilhante de inovação e engenhosidade na busca por soluções mais eficientes e eficazes.
A importancia da raiz quadrada no ambinete 3D
A importância da raiz quadrada em um ambiente 3D está principalmente relacionada ao cálculo de distâncias e vetores no espaço tridimensional. Em muitos algoritmos e técnicas de renderização, como cálculos de iluminação, sombreamento, detecção de colisão e transformações geométricas, é comum encontrar operações que envolvem a raiz quadrada.
No contexto de cálculo de distâncias, a raiz quadrada é essencial para determinar a magnitude de um vetor ou a distância entre dois pontos no espaço tridimensional. Isso é fundamental em aplicações como detecção de colisão, onde é necessário verificar se dois objetos estão próximos o suficiente para interagir.
Além disso, em técnicas de iluminação e sombreamento, a raiz quadrada é frequentemente usada para calcular a atenuação da luz com base na distância entre a fonte de luz e o ponto de superfície. Isso é crucial para simular efeitos realistas de luz e sombra em ambientes 3D.
Em suma, a capacidade de calcular rapidamente a raiz quadrada de números é fundamental para o desempenho e a precisão de muitos algoritmos e técnicas usados na renderização e na manipulação de objetos em um ambiente tridimensional.
O código abaixo exemplifica uma das importância da raiz quadrada para detectar colisões:
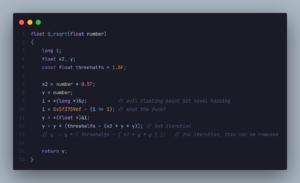
Por dentro do algoritmo
O algoritmo em questão, conhecido como “Fast Inverse Square Root” ou pela sigla “Q_rsqrt”, desempenha um papel crucial na otimização de cálculos envolvendo física, luz e reflexos em motores de processamento 3D, especialmente em jogos. Sua principal função é calcular o inverso da raiz quadrada de um número de forma rápida e eficiente.
Esse algoritmo se destaca por sua capacidade de realizar essa operação complexa de maneira extremamente eficaz, o que é essencial em ambientes onde o desempenho é crítico, como em jogos de computador. Ao fornecer uma solução rápida para calcular o inverso da raiz quadrada, o algoritmo Q_rsqrt permite que os motores gráficos 3D realizem cálculos complexos de forma mais eficiente, garantindo uma experiência de jogo suave e imersiva para os jogadores.
Dessa forma, o algoritmo Q_rsqrt se tornou uma peça fundamental na otimização de motores de processamento 3D, contribuindo significativamente para o desenvolvimento de jogos e outras aplicações que exigem cálculos intensivos em ambientes tridimensionais. Sua eficácia e eficiência o tornam uma ferramenta valiosa para desenvolvedores que buscam maximizar o desempenho de seus sistemas gráficos.
Vamos examinar o algoritmo:
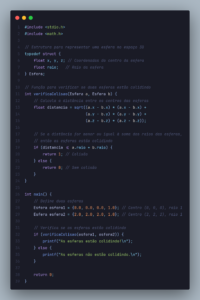
É verdade, à primeira vista, o código pode parecer simples, consistindo em apenas algumas linhas com valores declarados. No entanto, a verdadeira complexidade e genialidade do algoritmo estão escondidas nas entrelinhas.
O que torna o algoritmo tão impressionante é sua capacidade de calcular o inverso da raiz quadrada de um número de maneira extremamente eficiente, com um desempenho excepcionalmente rápido. Por trás das poucas linhas de código, há um processo matemático intrincado e altamente otimizado, projetado para minimizar o tempo de computação enquanto mantém uma precisão aceitável.
A genialidade do algoritmo reside na maneira como ele manipula os bits do número de ponto flutuante para realizar o cálculo de forma eficiente, aproveitando padrões numéricos específicos para evitar operações computacionalmente custosas, como a raiz quadrada.
Assim, embora o código possa parecer simples à primeira vista, sua verdadeira engenhosidade e complexidade só podem ser apreciadas quando se entende a profundidade do processo matemático e a sutileza das otimizações implementadas. É essa habilidade de alcançar um desempenho excepcional com uma implementação aparentemente simples que torna o algoritmo tão notável e valioso em contextos onde o tempo de computação é crucial.
Explorando o algoritmo
Para compreender profundamente o algoritmo, é essencial explorar alguns conceitos fundamentais tanto de computação quanto de matemática.
O algoritmo se baseia na manipulação de bits e na aproximação de valores, fazendo uso do padrão IEEE 754, que define a representação binária de números em ponto flutuante. Ao extrair e manipular os bits do número de entrada, o algoritmo inicia sua jornada.
Uma etapa crucial é a aproximação do logaritmo por base 2 do número, o que simplifica significativamente os cálculos subsequentes. Essa aproximação é realizada utilizando operações bitwise e truques matemáticos, permitindo uma execução rápida e eficiente.
Além disso, a aplicação do método de Newton para encontrar uma aproximação mais precisa do valor contribui para a eficiência do algoritmo. Esse método iterativo é empregado para refinar a aproximação inicial, levando a um resultado mais exato em menos iterações.
Ao combinar esses conceitos de manipulação de bits, aproximação de valores e o método de Newton, o algoritmo Q_rsqrt consegue calcular o inverso da raiz quadrada de um número de forma extremamente eficiente, proporcionando um desempenho excepcional em ambientes onde o tempo de computação é crítico, como em motores gráficos 3D de jogos.
Portanto, ao entender a fundo esses conceitos e como são aplicados no algoritmo, podemos apreciar sua complexidade e genialidade, e entender por que ele se destaca como uma ferramenta valiosa na otimização de cálculos em ambientes computacionais exigentes.
Por dentro da matematica
A manipulação de bits é uma técnica fundamental na computação, onde toda a informação é representada por sequências de 0s e 1s, chamadas de bits. Esses bits são agrupados para formar diferentes tipos de dados, como bytes, que são grupos de 8 bits. O primeiro passo do algoritmo é converter o número de ponto flutuante em uma representação binária e, em seguida, manipular os bits desse número para obter uma aproximação rápida da raiz quadrada inversa.
Resumidamente, a manipulação de bits envolve realizar cálculos matemáticos em um nível mais baixo do que as operações aritméticas, alterando diretamente os padrões de 0s e 1s que representam os números. Essa técnica permite manipular os valores de forma eficiente e rápida, o que é especialmente útil em situações onde o desempenho é crítico, como em motores de jogos 3D.
A imagem abaixo exemplifica como a manipulação de bits pode ser usada para realizar operações como deslocamento de bits para a esquerda e para a direita, além de operações lógicas como AND, OR e XOR.
 Nessa imagem, podemos ver como os bits de dois números são manipulados usando diferentes operações de bit a bit para produzir um resultado específico. Essas operações de manipulação de bits são a base para muitos algoritmos eficientes e poderosos na computação.
Nessa imagem, podemos ver como os bits de dois números são manipulados usando diferentes operações de bit a bit para produzir um resultado específico. Essas operações de manipulação de bits são a base para muitos algoritmos eficientes e poderosos na computação.
Conforme ilustrado, deslocar um dígito para a esquerda dobra o valor, enquanto deslocá-lo para a direita o reduz pela metade, embora isso possa resultar em imprecisões quando arredondamentos são necessários. No caso do algoritmo, as variáveis do tipo float, como o valor Y, não possuem recursos integrados para manipulação de bits na linguagem C, pois não foram originalmente projetadas com essa finalidade. No entanto, variáveis do tipo long foram concebidas para tal manipulação.
Para contornar essa limitação, é necessário converter o endereço de memória da variável. Dessa forma, é possível manipular a linguagem C para alterar o tipo da variável, enquanto preserva o seu valor original, conforme exemplificado na linha “i = 0x5f3759df – (i >> 1)”.
IEEE 754 e Padrões de Ponto Flutuante: O padrão IEEE 754 é uma especificação fundamental para a representação e aritmética de números em ponto flutuante em sistemas computacionais. Ele define formatos padronizados para representar números em ponto flutuante, além de especificar operações aritméticas para manipular esses números. O IEEE 754 é amplamente adotado em computadores modernos e desempenha um papel essencial na representação e manipulação precisa de números reais em diversas aplicações computacionais.
Os números em ponto flutuante seguem uma notação científica normalizada composta por três partes principais:
- Sinal: Um único bit que indica se o número é positivo ou negativo.
- Expoente: Um campo de bits que representa o expoente do número.
- Mantissa (ou Fração): Um campo de bits que representa a parte fracionária do número.
Esse conceito é aplicado na linha “i = 0x5f3759df – (i >> 1)” do algoritmo. Utilizando a manipulação de bits, podemos encontrar tanto a raiz quadrada quanto o quadrado de um número. Da mesma forma, manipulando o expoente, podemos dobrar o valor do número ou dividi-lo pela metade, assim como encontrar a sua raiz quadrada. Portanto, ao manipularmos esse padrão, podemos armazenar o valor desejado como uma notação científica, permitindo operações eficientes e precisas em sistemas computacionais.
Aproximação do Logaritmo por 2: Uma das partes essenciais do algoritmo é a aproximação do logaritmo por 2 do número de entrada, expressa em “i = 0x5f3759df – (i >> 1)”. Esse cálculo é realizado por meio de manipulações bit a bit e truques matemáticos. O propósito é simplificar os cálculos subsequentes, tornando-os mais rápidos e eficientes, uma vez que a representação binária de um número está intimamente relacionada ao seu logaritmo na base 2.
Embora o uso do logaritmo ainda exija uma divisão, o que poderia tornar o código mais lento, podemos contornar esse problema movendo os bits para a esquerda novamente, utilizando o mesmo método mencionado anteriormente. O valor definido como 0x5f3759df pode parecer surgir do nada, mas é resultado de um processo de “padronização” derivado da equação original.
Assim, podemos aplicar novamente os conceitos do padrão IEEE para extrair o valor da mesma maneira que anteriormente, conforme exemplificado na linha “y = (float)&i”, obtendo seu valor decimal. No entanto, é importante destacar que esse método produz um valor aproximado que requer tratamento adicional em seguida.
Método de Newton: Também conhecido como Método Newton-Raphson, é uma técnica iterativa amplamente utilizada para encontrar raízes de equações não lineares. Este método é especialmente eficaz quando a derivada da função é conhecida ou pode ser facilmente calculada. Funciona aproximando iterativamente a raiz da função por meio de tangentes à curva da função.
A essência do Método de Newton é começar com uma estimativa inicial da raiz e, em seguida, utilizar a tangente à curva da função nesse ponto para obter uma estimativa melhorada da raiz. Esse processo é repetido até que a diferença entre as estimativas sucessivas seja menor que uma determinada tolerância.
Um exemplo prático do Método de Newton é encontrar a raiz quadrada de um número. Seja f(x)=x2−Sf(x)=x2−S, onde SS é o número cuja raiz quadrada queremos encontrar. A raiz quadrada de SS é o valor de xx onde f(x)=0f(x)=0.
O Método de Newton segue a seguinte iteração:
xn+1=xn−f(xn)f′(xn)xn+1=xn−f′(xn)f(xn)
Onde:
- xn+1xn+1 é a próxima estimativa da raiz.
- xnxn é a estimativa atual da raiz.
- f(xn)f(xn) é o valor da função na estimativa atual.
- f′(xn)f′(xn) é a derivada da função na estimativa atual.
A execução de “y = y * ( threehalfs – ( x2 * y * y ) )” nada mais é do que a aplicação do Método de Newton. Ele é um algoritmo que busca uma aproximação mais precisa de valores, “adivinhando” o valor mais próximo com base na margem de erro.
Ao combinar todos esses conceitos, obtemos uma implementação inteligente, onde, mesmo que o algoritmo exija uma divisão, conseguimos evitá-la e ainda assim chegar ao valor desejado com uma velocidade incomparável.
O código a baixo é um exemplo de implementação desse método na linguagem C:
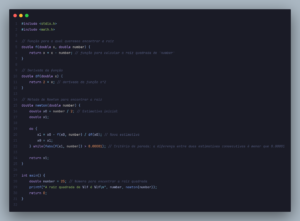
Conclusão
O algoritmo utilizado no Quake 3 Arena é um exemplo notável de engenharia de software e aplicação matemática. Sua habilidade em executar cálculos complexos de maneira rápida e eficiente mudou permanentemente a maneira como os jogos são desenvolvidos.
Espero que este artigo tenha elucidado a importância desse algoritmo revolucionário e que o tempo dedicado à sua leitura tenha sido produtivo. Agradeço sinceramente pela sua atenção.




 Nessa imagem, podemos ver como os bits de dois números são manipulados usando diferentes operações de bit a bit para produzir um resultado específico. Essas operações de manipulação de bits são a base para muitos algoritmos eficientes e poderosos na computação.
Nessa imagem, podemos ver como os bits de dois números são manipulados usando diferentes operações de bit a bit para produzir um resultado específico. Essas operações de manipulação de bits são a base para muitos algoritmos eficientes e poderosos na computação.